API tutorial
This page contains a simple tutorial on how to connect a learning algorithm to
a real system under test (SUT). As an example we will learn the behavior of a
Java class. This class Pool implements a pool of objects.
The pool is implemented around a set. Thus, each object can only be contained
once. The pool has methods to
- add an object
- remove an object
- test if the pool is empty
The source of the implementation looks like:
public class Pool {
private Set<Object> pool = new HashSet<Object>();
public void add(Object o) {
pool.add(o);
}
public void remove(Object o) {
pool.remove(o);
}
public boolean isEmpty() {
return pool.isEmpty();
}
}
Connecting to the system
Learning algorithms can not be connected directly to real systems. Learning algorithms use alphabets. A learning algorithm will formulate a test case that is to be executed on the system in an abstract language (as words that are build from the input alphabet). It will also expect the reaction of the system to be encoded into words over the output alphabet.
To connect a learning algorithm and a real system, we will need to have a test-driver, which translates input words into sequences of real actions (e.g., method calls) and real outputs (e.g., return values) into output words. In the test-driver, we first define these alphabets.
public class PoolTestDriver {
// input symbols
private static final Symbol O1_IN = new SymbolImpl("o1in");
private static final Symbol O2_IN = new SymbolImpl("o2in");
private static final Symbol O1_OUT = new SymbolImpl("o1out");
private static final Symbol O2_OUT = new SymbolImpl("o2out");
private static final Symbol ISEMPTY = new SymbolImpl("isempty?");
// input alphabet used by learning algorithm
public static final Alphabet SIGMA;
static
{
SIGMA = new AlphabetImpl();
SIGMA.addSymbol(O1_IN);
SIGMA.addSymbol(O2_IN);
SIGMA.addSymbol(O1_OUT);
SIGMA.addSymbol(O2_OUT);
SIGMA.addSymbol(ISEMPTY);
}
// return values
private static final Symbol TOP = new SymbolImpl("true");
private static final Symbol BOT = new SymbolImpl("false");
private static final Symbol NOOP = new SymbolImpl("-");
...
Here, single actions are of type
Symbol
(which is a Java Interface).
We here use
SymbolImpl,
a lightweight implementation of Symbol.
Each Symbol holds a user-defined object. In this tutorial we use plain strings
as user objects. Symbols are compared (and identified) using the equals()
method of the user object. We define one
Symbol
for each action we plan to
invoke on the SUT and for each answer we expect from the SUT. The input symbols
will be given to the learning algorithm in form of an
Alphabet.
Again, we use the basic implementation
AlphabetImpl,
that is provided by LearnLib. The
learning algorithms work with a flexible output alphabet. We therefore
can omit building an explicit output alphabet. In this example we will
learn the behavior of the pool for two objects that can be added or removed.
After defining the side of the test-driver that will be exposed to the learning algorithm later, we need some code to instrument the SUT. This code essentially consists of two parts:
- execution of symbols
- reset
The learning algorithm will need to have a means of executing words of inputs on the system and get back words of outputs. In the test-driver we therefor a method that allows the execution of single symbols on the SUT. The method simply translates input symbols into method calls and the results of method calls into output symbols.
The learning algorithm will further require a means of reseting the SUT into its initial state. We provide this by simply creating a new instance of the SUT each time a reset is required.
...
// system under test
public Pool pool;
// local test variables
private final String o1 = "o1";
private final String o2 = "o2";
public Symbol executeSymbol(Symbol s) {
if (s.equals(O1_IN)) {
pool.add(o1);
return NOOP;
} else if (s.equals(O2_IN)) {
pool.add(o2);
return NOOP;
} else if (s.equals(O1_OUT)) {
pool.remove(o1);
return NOOP;
} else if (s.equals(O2_OUT)) {
pool.remove(o2);
return NOOP;
} else if (s.equals(ISEMPTY)){
return pool.isEmpty() ? TOP : BOT;
}
return null;
}
public void reset() {
this.pool = new Pool();
}
}
Oracles
The test-driver still contains very SUT-specific code. To make explicit the
different concerns when connecting to a real system we split the implementation
of the test-driver and the
Oracle.
A learning algorithm will expect an instance of Oracle as connection
to the system. As the concrete realization of an oracle typically depends on
the concrete SUT to be learned, one will not find a general basic
implementation of an Oracle in LearnLib.
public class PoolOracle implements Oracle {
private PoolTestDriver testDriver;
public PoolOracle() {
testDriver = new PoolTestDriver();
}
@Override
public Word processQuery(Word query) throws LearningException {
...
An oracle has to implement only one method: Word processQuery(Word query).
In this example we implement this method to only
- reset the SUT
- iterate over the query and execute it step-wise on the SUT (via the test-driver)
...
public Word processQuery(Word query) throws LearningException {
Word trace = new WordImpl();
testDriver.reset();
for (Symbol i : query.getSymbolList()) {
Symbol o = testDriver.executeSymbol(i);
trace.addSymbol(o);
}
return trace;
}
}
Learning the behavior of the Pool
We now have everything at hand to learn the behavior of our SUT.
Logging
LearnLib provides a logging framework that allows
you to log output to different facilities. For each
LoggingAppender
that is added to the logging system you can assign a threshold level. Only messages
above this level will be passed to the according appender. We here use a
PrintStreamLoggingAppender
to log to System.out and second appender that logs to a html file.
LearnLog.addAppender(new PrintStreamLoggingAppender(LogLevel.INFO,System.out));
LearnLog.addAppender(new HtmlLoggingAppender(LogLevel.DEBUG,
"/tmp/learn.html", false, false, false));
Setup
Now, let us create the oracle, the learning algorithm, and the equivalence algorithm. We here use a W-Method conformance test to simulate equivalence queries and initialize it with N=4 (where N is an upper bound on number of states the SUT can have). In this example we chose this bound to be tight - which for real black-boxes normally one cannot! LearnLib comprises a number of algorithms for equivalence approximation.
As learning algorithm we chose the
ObservationPack
algorithm (there are several other learning alorithms implemented in
LearnLib).
To both the learning algorithm and the equivalence algorithm we pass the oracle.
To the learning algorithm we also pass the input alphabet.
The equivalence algorithm will later construct the input alphabet
on-the-fly from the hypothesis.
// create oracle for mutex Oracle testOracle = new PoolOracle(); EquivalenceOracle eqtest = new WMethodEquivalenceTest(4); eqtest.setOracle(testOracle); Learner learner = new ObservationPack(); learner.setOracle(testOracle); learner.setAlphabet(PoolTestDriver.SIGMA);
Main loop
In the main loop the actual learning round are carried out. Invoking the
learn() method on a learning algorithm will make the algorithm
complete the actual round of learning. After completion, the current hypothesis
is passed to the equivalence algorithm. In case a counterexample is found,
this will be passed back to the learning algorithm.
If no counterexample is found, the main loop will be left and the learned
model will be persisted into a file the dot-utility of
Graphviz can process using the
DotUtil
class.
boolean equiv = false;
while (!equiv)
{
// learn one round
learner.learn();
Automaton hyp = learner.getResult();
logger.log(LogLevel.INFO, "hypothetical states: " +
hyp.getAllStates().size());
// search for counterexample
EquivalenceOracleOutput o = eqtest.findCounterExample(hyp);
if (o == null) {
equiv = true;
continue;
}
learner.addCounterExample(o.getCounterExample(), o.getOracleOutput());
}
DotUtil.writeDot(learner.getResult(), new File("/tmp/learnresult.dot"));
Running the example
Below you see the output the PrintStreamLoggingAppender will produce
on System.out for this example. It is splitted into several parts.
Furthermore you can see what the hypothesis and data structure of the
algorithm look like at the end of every round.
Round 1
======================================================================== [INFO] Closing Table ======================================================================== ------------------------------------------------------------------------ [INFO]Splitting Component suffix: [isempty? ] New access sequence: [o1in ] New trace: [false ] Old accesss sequence: [] Old trace: [true ] ------------------------------------------------------------------------ [INFO] New state: o1in ======================================================================== [INFO] Checking Consistency ======================================================================== [INFO] hypothetical states: 2
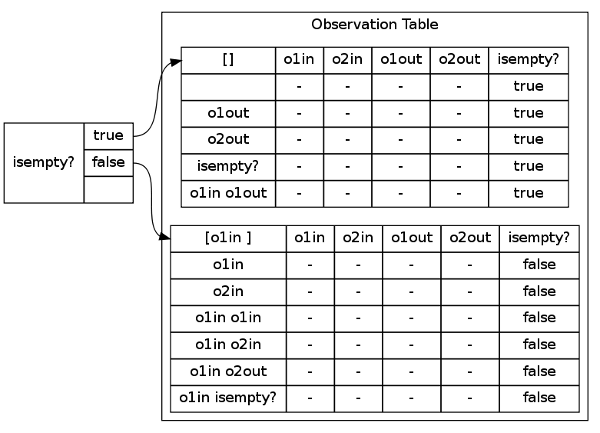
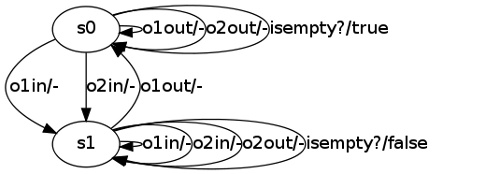
Round 2
======================================================================== [INFO] Equivalence Query ======================================================================== ------------------------------------------------------------------------ [INFO]W-method conformance-test setup hypothesis size (n): 2 maximal size (N): 4 alphabet size (|A|): 5 prefixtree size (|p|): 11 suffix set size (|z|): 1 max. add. distance (w): 2 test size: SUM ( |p| * (|A|^i) * |z| ), for all 1 <= i <= w test size: 330 ------------------------------------------------------------------------ ======================================================================== [INFO] Analyzing Counterexample ======================================================================== ======================================================================== [INFO] Closing Table ======================================================================== ------------------------------------------------------------------------ [INFO]Splitting Component suffix: [o1out isempty? ] New access sequence: [o2in ] New trace: [false ] Old accesss sequence: [o1in ] Old trace: [true ] ------------------------------------------------------------------------ [INFO] New state: o2in ======================================================================== [INFO] Checking Consistency ======================================================================== ======================================================================== [INFO] Analyzing Counterexample ======================================================================== [INFO] [o2in o1out isempty? ] is not a counterexample [INFO] hypothetical states: 3
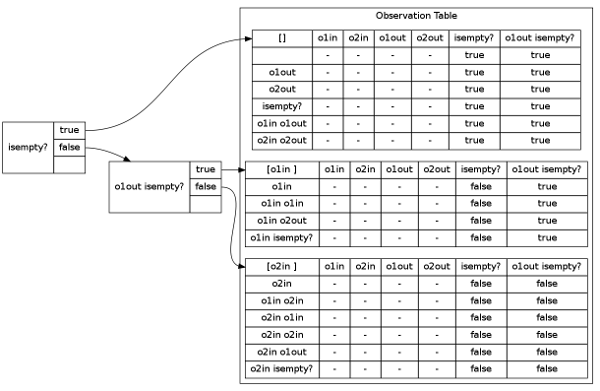
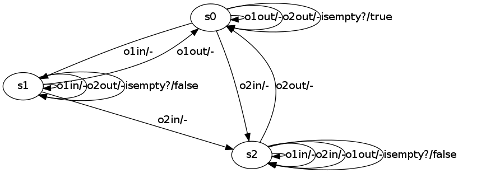
Round 3
======================================================================== [INFO] Equivalence Query ======================================================================== ------------------------------------------------------------------------ [INFO]W-method conformance-test setup hypothesis size (n): 3 maximal size (N): 4 alphabet size (|A|): 5 prefixtree size (|p|): 16 suffix set size (|z|): 2 max. add. distance (w): 1 test size: SUM ( |p| * (|A|^i) * |z| ), for all 1 <= i <= w test size: 160 ------------------------------------------------------------------------ ======================================================================== [INFO] Analyzing Counterexample ======================================================================== ======================================================================== [INFO] Closing Table ======================================================================== ------------------------------------------------------------------------ [INFO]Splitting Component suffix: [o2out isempty? ] New access sequence: [o1in o2in ] New trace: [false ] Old accesss sequence: [o2in ] Old trace: [true ] ------------------------------------------------------------------------ [INFO] New state: o1in o2in ======================================================================== [INFO] Checking Consistency ======================================================================== ======================================================================== [INFO] Analyzing Counterexample ======================================================================== [INFO] [o2in o1in o2out isempty? ] is not a counterexample [INFO] hypothetical states: 4
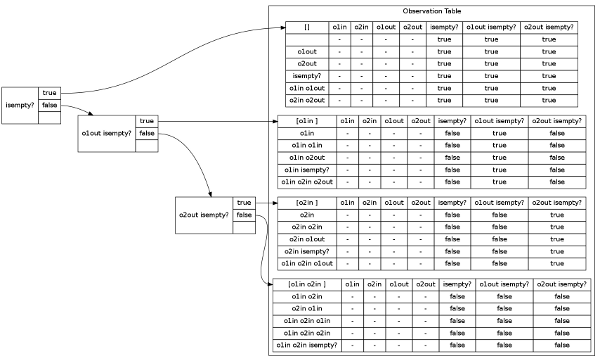
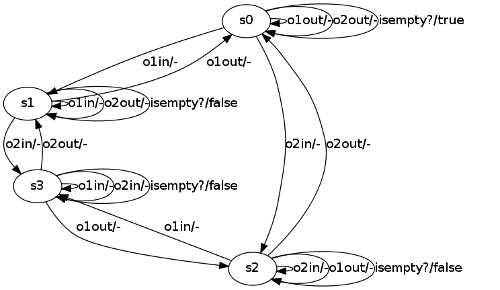
Last Equivalence Query
The last W-Method test contains 0 tests as the hypothesis has already 4 states (which we set as an upper bound to the number of states in the real system).
======================================================================== [INFO] Equivalence Query ======================================================================== ------------------------------------------------------------------------ [INFO]W-method conformance-test setup hypothesis size (n): 4 maximal size (N): 4 alphabet size (|A|): 5 prefixtree size (|p|): 21 suffix set size (|z|): 3 max. add. distance (w): 0 test size: SUM ( |p| * (|A|^i) * |z| ), for all 1 <= i <= w test size: 0 ------------------------------------------------------------------------ [INFO] DONE!!